Tech Stuff - Sound Primer

This primer describes the primary characteristics of a note or sound. It is not exhaustive. Partly, because life is not long enough. Partly, because there are always exceptions, for example, the Gamelin has very special audio characteristics which are not covered even if we knew what they were - which we don't. Partly, because you (we) would get lost in a mass of detail without getting the overall picture (nifty excuse). Partly, because, to paraphrase Donald Rumsfeld, we don't know what we don't know. Kinda.

Contents

Note, Pitch, Frequency and the ADSR Envelope
Fundamentals, Harmonics, Overtones and Partials
Loudness and Sound Power

Note, Pitch and Frequency

When we play a single note, say C4 (middle C on a piano), it has a pitch a.k.a. its fundamental frequency. In the case of C4 this is 262Hz which means it sends out sound waves at this frequency. From observation we know that the same note, say, C4 on a piano and a saxophone sound very different (well, to most of us). We need an explanation.

Turns out the explanation is not trivial. When an instrument is played: we hit something, saw something or blow into something, the physical design characteristics give it all manner of sound properties (this is true of the human voice as well). The sound characteristics of each instrument (or each noise producing device) create what is usually called the intrument's timbre - a sort of catch-all term which encompasses all the individual bits (highly technical term) or elements that collectively make up the instrument's unique sound.

The act of creating the sound creates multiple harmonics and overtones (covered in the next section) and what is called the Amplitude Envelope or in super-tech terms the ADSR (Attack, Decay, Sustain, Release) envelope. Such an ADSR envelope for a single note would look something like that shown below:

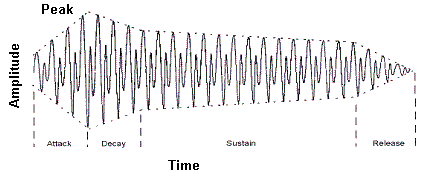
This is a Time Domain view of an ADSR. For more detail on Instrument ADSRs see Digital Sound - ADSR.

Each instrument (again, the human voice is an instrument) has a different ADSR Envelope - sustain times may be longer, attack times shorter, etc. - and some instruments, such as the piano, can vary the envelope (by using the sustain pedal) from note to note. Violinists seem to be especially clever at changing the ADSR envelope by doing strange things with their fingers while moving the bow. The important point to note (OK, OK) is that the frequency of the note is constant within the envelope it is the amplitude (kinda related to loudness) that changes. Within this ADSR envelope we seem to be especially sensitive to the attack part (which by the way, in the interests of sanity, is greatly simplified in the above diagram). Finally, it gets worse - much, much worse - each harmonic and overtone also has an ADSR envelope and they do not have the same characteristics even for the same instrument. Oh, stop the pain.

Fundamentals, Harmonics, Overtones and Partials

Harmonics: When we play a single note, say, C4 (middle C on a piano) it has a pitch (a.k.a fundamental frequency). In the case of C4 this is 262Hz. But the instrument also generates harmonics or secondary waves (sometimes erroneously - IOHO - called overtones) which have frequencies at integer multiples, 2 times, 3 times etc. of the fundamental frequency. Thus, the note C4, from any instrument, will generate a fundamental frequency of 262 Hz (also called - confusingly - the first harmonic) and additional harmonics at 524 Hz (2 x 262 - the second harmonic), 786 Hz (3 x 262 - the third harmonic), 1048 Hz (4 x 262 - the 4th harmonic) etc. essentially forever but each - generally, but not universally - getting weaker. Each harmonic also has a ADSR (Amplitude) envelope. The physical design characteristics of the instrument (including the human's vocal chords) control the number and amplitude of the harmonics. (Further, instruments can generate strong and weak harmonics unrelated to their order, thus in a particular instrument the 3rd harmonic may be weak but the 4th strong.) To illustrate harmonic production with specific examples, the clarinet due to its physical design suppresses even-numbered harmonics, whereas a saxophone does not, even though both are reed based instruments. Harmonics are always at or higher than the Fundamental Frequency.

Overtones: Overtones are additional sound waves created by the design of the instrument and are defined generically as any (including non-integer) multiples of the fundamental frequency thus, for example, they could be at 1.3 or 7.4 times the fundamental frequency. For string instruments (piano, guitar, violin etc.) and long thin instruments the first few harmonic and overtones do coincide and then start to diverge at higher values. Bells are the most notorious since apparently the harmonics and overtones never coincide. Each overtone also has a ADSR (Amplitude) envelope. Harmonics have an integer relationship with the fundamental and are always pleasing (or harmonious) to the ear whereas overtones because they may have a non-integer relationship (though can coincide with the harmonics as noted) may have an unpleasant, or dissonant, effect. Harmonics are almost always good, overtones are not always good. Overtones are always higher than the Fundamental Frequency.

Some documentation uses the term overtone as if it were synonymous with harmonic. We find this confusing since a harmonic has a integer raltionship with the Fundamental Frequency whereas an overtone may, or may not, have an integer relationship. In cases where the term overtone is used to include integer relationships it is differentiated by using the composite, and in our view clumsy, term Harmonic Overtone.

Undertone: A note below the Fundamental Frequency, having a numeric (integer or non-integer) relationship. Special playing techniques typically have to used to generate undertones. They do not occur naturally on most instruments. (The pipe organ is one of the exceptions).

Partials: The term Partial is applied to everything - fundamental tone, harmonics, overtones - everything - since individually they are only a part of the complete musical note. Thus, one could say that a musical note is composed of all its partials.

Counting: When we count harmonics the fundamental frequency = 1st harmonic, then at twicee the fundamental frequency we have the 2nd harmonic etc., etc.. When counting overtones we do not count the fundamental frequency thus, where and overtone and a harmonic coincide the 2nd harmonic = 1st overtone, the 3rd harmonic = 2nd overtone etc. The first partial is the fundamental, the second partial is the 2nd harmonic (which may also be the 1st overtone) etc. All very simple really.

Timbre: We know from observation that, say, C4 from a soprano and a piano sound significantly different - they each have a different timbre (feel). In general, the timbre (or difference in tone quality) comes from the presence and loudness (amplitude) of harmonics and overtones and the ADSR envelope. The vibrational characteristics of each sound producer (instrument, voice etc.) are different and not all will generate harmonics (or overtones) at the same amplitude or with the same ADSR (Amplitude) envelope.

Sound Reproduction: When an instrument plays a note its physical characteristics will determine the number and amplitude of the harmonics and overtones. When that note is recorded all reference to the original properties of the instrument are lost. We do not record a saxophone playing C4, we record the sounds that a saxophone makes playing C4. A subtle but possibly important difference. Thus, when the sound is played back the harmonics and overtones captured by the recording become essentially fundamentals which may generate new harmonics and overtones with the characteristics, not of the original sound producer (instrument), but of the playback system.

Health Warning: The terms harmonic, overtone and partial are used with wildly varying degrees of precision in digital audio and general audio literature. For instance, you will frequently see harmonics described as overtones, including by otherwise very knowledgeable authors, which, IOHO, is at best confusing and almost always incorrect since as we have seen only for certain instrument types do they coincide and then typically only at lower harmonics. Finally, you will see the term partial applied to a harmonic which is strictly correct but usually imprecise and normally not terribly edifying. But it probably and regrettably achieves its subliminal goal of confusion for the poor reader and underlines the deity-like knowledge of the writer.

Loudness and Sound Power

Sound is normally measured in decibels (dB). This is widely used but relatively meaningless as a term since the dB is simply the ratio of two values and as such is, of itself, dimension-less. It needs qualification to mean something. In acoustics what is written as dB normally means dB(SPL) where SPL is the Sound Pressure Level. Simply put SPL means the pressure that is measured at the listener's ears. In the real world this is a positive number so a dB(SPL) of 50-55 would be the typical ambient noise level in a normal office (which does not include ours which frequently appears to approach jet take-off noise levels). In the digital world db(SPL) would normally be a negative value with 0dB being the point at which distortion would typically occur after it has been put through a DAC (Digital to Analog Converter) and then amplified for output on a loudspeaker system.

So dB (or more correctly dB(SPL)) is the measure of loudness, right?

Not exactly. First, loudness is a subjective measure. If you spent your adolescent years in noisy discos or clubs you may find the sound of a jet fighter taking off under full-power 10 meters away to be a vague rumble, whereas someone who grew up in the arctic circle may find the sound of a New Yorker's normal speech level to be approaching the pain threshold. Second, it turns out that we humans are jolly clever and have evolved a hearing system that is more sensitive to sounds in certain frequencies than in others. In general, we are more sensitive to sound in the range 400Hz to 5KHz with particular sensitivity in the range 2 - 4KHz. This variable sensitivity could be, speculatively, attributed to the sound of danger or other potentially unpleasant circumstances. It would be reasonable to speculate over the long span of history we would have become especially sensitive to, say, the sound of a bear crashing though the woods towards us. While we are in the realm of pure speculation it may also we worth observing that most men seem relatively insensitive to the sound of a baby crying at 4am (frequencies unknown) whereas most women are not. Although this phenomenon may be more related to a higher order function than simple hearing.

The human sensitivity to frequencies - and their perceived level of loudness - are described by a series of Fletcher-Munson curves (after the guys who developed them) and is measured in phons as shown below:

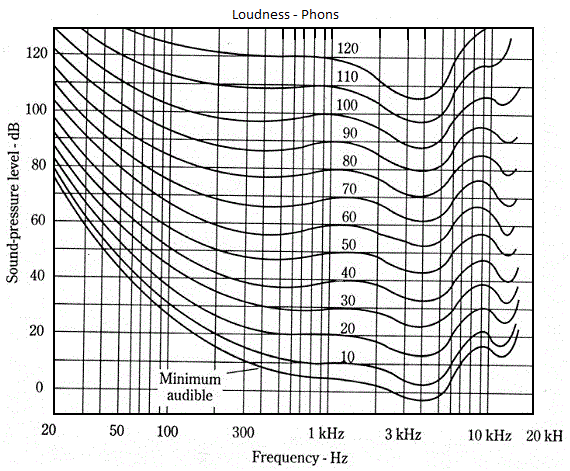
The graph shows that for a given level of loudness, say 40 phons, then at a frequency of around 3KHz the sound would only have to be around 32-33 dB(SPL) whereas to appear equally loud at a frequency of 20Hz it would have to be over 90 dB(SPL). A variety of equalization algorithms have been developed to process recorded material taking this perception phenomenon (generically known as physcoacoustics) into account - A-Weighting, B-Weighting and C-Weighting being the most common. Indeed if such an algorithm has been applied to compensate (or equalize) you will sometimes see the dB values written as dB(A) or dB(B) or dB(C) depending an the applied algorithm.

Sound Power and Hearing Damage

We have have made various comments throughout this and other pages that allude to hearing range such as "unless you spend time in noisy clubs". These comments are not entirely frivolous. Exposure to noise can cause damage to hearing. Various health and safety jurisdictions have regulations concerning timed exposure to noise levels in order to reduce the risk of hearing impairment. In general, the table below shows the maximum time that humans can be exposed to certain sound levels before running the risk of hearing damage.

dB(A)	Max. Exposure Time	Notes
82	16 hours
85	8 hours
88	4 hours
91	2 hours
94	1 hour	Typical club is ~96dB(A)
97	30 minutes
100	15 minutes
103	7.5 minutes	Extreme club is ~104dB(A)

---

Problems, comments, suggestions, corrections (including broken links) or something to add? Please take the time from a busy life to 'mail us' (at top of screen), the webmaster (below) or info-support at zytrax. You will have a warm inner glow for the rest of the day.